Math 2014 Algorithms - 3 Graph Reachability

3.1 The Graph Reachability Problem

Definition 3.1 (The Graph Reachability Problem) Given a directed graph \(G = (V,A)\) and a node \(s\). Find the set \(M\) of all nodes that are reachable from \(s:\)

i.e., all nodes that are connected to \(s\).

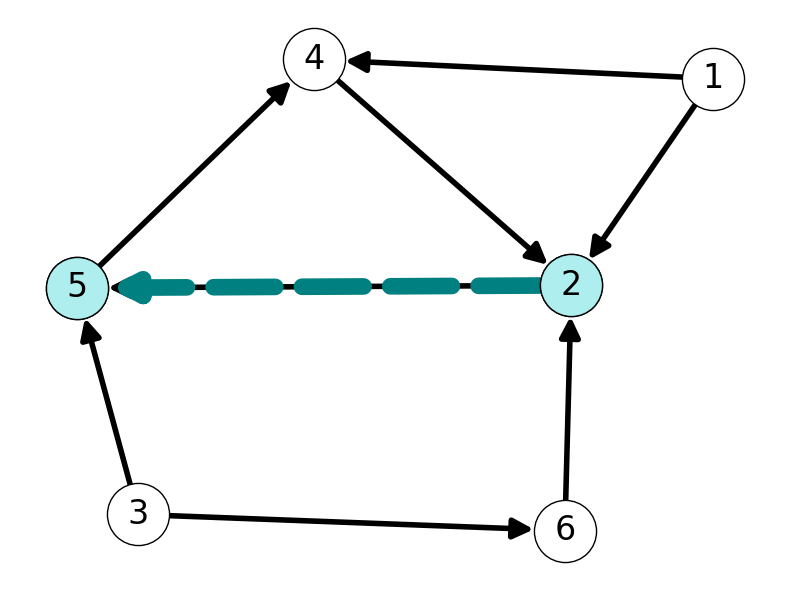
Example 3.1 Consider the graph \(G\) given in Figure 2 (a). The set of reachable nodes from \(s=1\) is \(M = \{1,2,4,5\}\) (see Figure 2 (b)).

3.2 Algorithm Idea

The following steps give an intuitive process for finding reachable nodes from a given node \(s\).

Explore \(s\): start from \(s\) and follow the arcs in its forward star to find its neighbors.
Repeat with each neighbor of neighbors of \(s\).
Repeat with neighbor of neighbors of neighbors of \(s\), etc.

3.3 Illustration of Idea

Let’s apply this idea for the graph \(G\) given in Figure 2 (a) with source node \(s = 1\).

3.3.1 Step 1

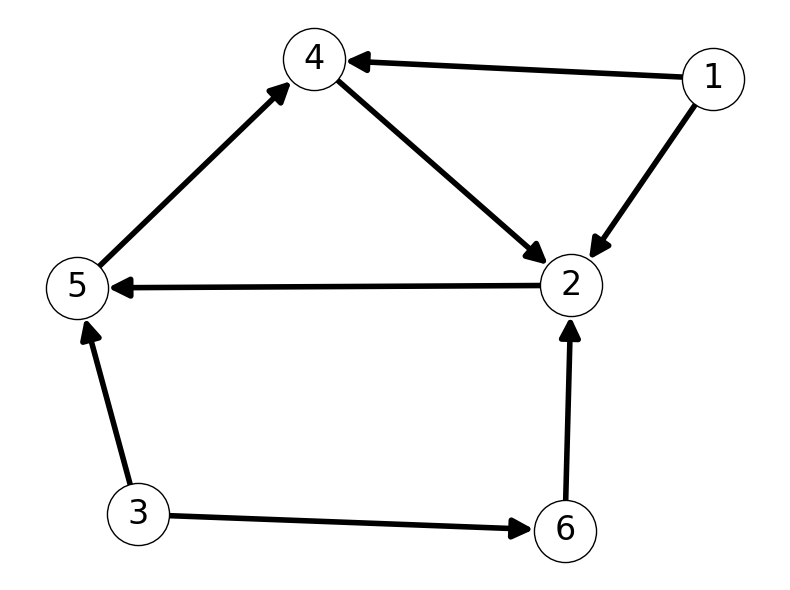
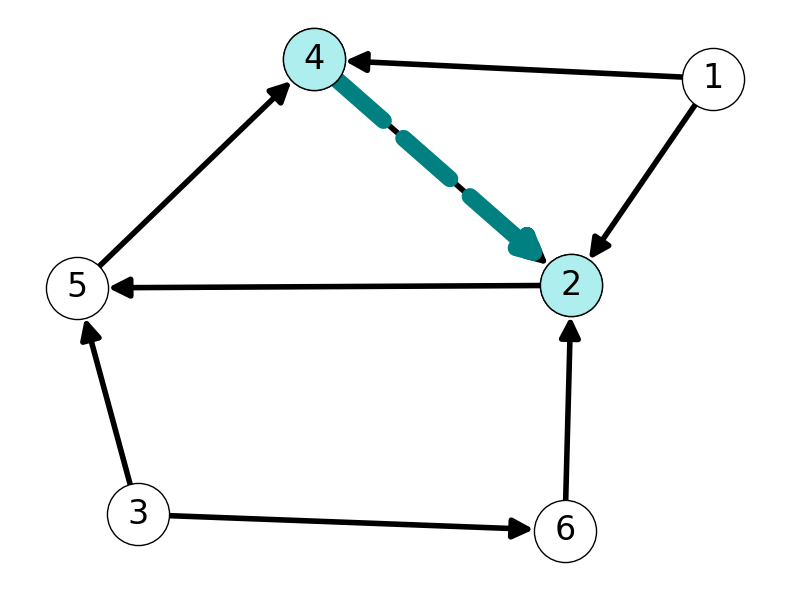
The forward star of \(s\) is \[ \delta^+(\{1\}) = \{(1,2), (1,4)\}. \] This implies that \(2\) and \(4\) are both reachable from \(1\). That is, \(M\) contains \(\{1,2,4\}\). See Figure 2 (a).

3.3.2 Step 2

We need to explore further from nodes \(2\) and \(4\). Let’s start with \(2\). The only node adjacent to \(2\) is node \(5\). We can conclude that \(M\) contains \(\{1,2,4,5\}\). See Figure 2 (b).

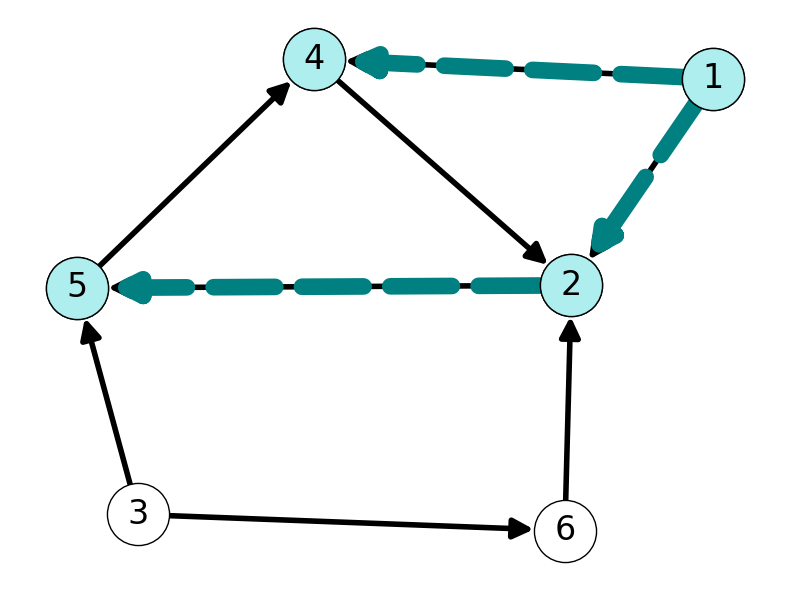
3.3.3 Step 3

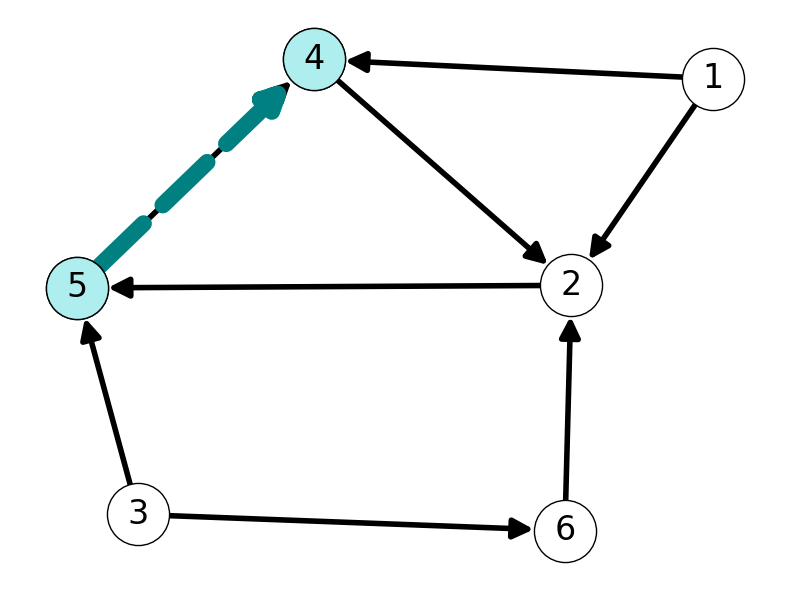
Let’s explore from node \(4\): \(2\) is the only node adjacent to \(4\). Our partially computed reachable set \(M\) is unchanged. See Figure 2 (c).

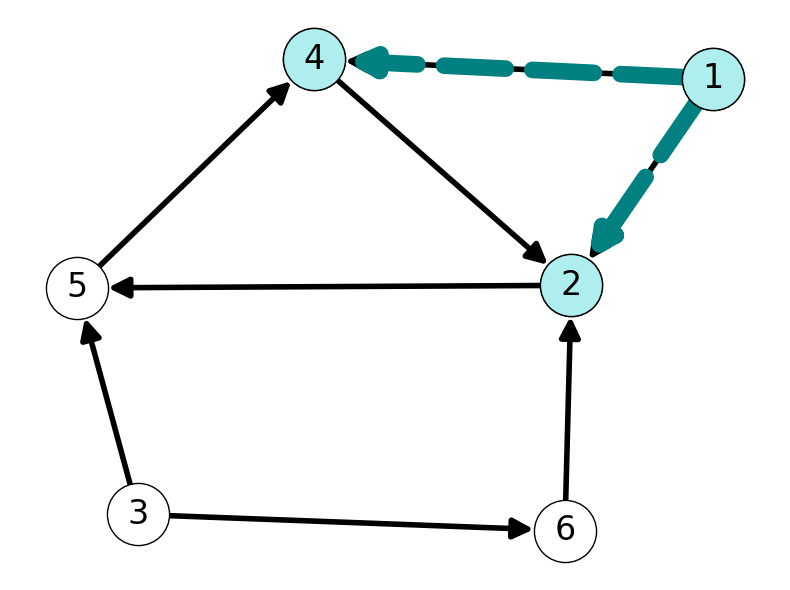
3.3.4 Step 4

We haven’t explored from node \(5\) yet. Let’s do that now. The only arc incident with \(5\) is \((5,4)\). Thus, \(4\) is adjacent to \(5\) and, hence, reachable from \(1\). We already knew that \(4\) is in \(M\), so \(M\) is unchanged. See Figure 2 (d).

3.3.5 Step 5

We have a choice of nodes to explore from: \(\{2, 4, 5\}\). We have already explored each of these nodes and appear to be stuck in a loop. Can we conclude that \(M = \{1,2,4,5\}\)?

(a) Step 1: \(M \supseteq \{1,2,4\}\) so far

3.4 Avoiding Cycles

3.4.1 Goal and Notation

We need to avoid exploring nodes we have already explored.

Let’s define \(M\) as the set of nodes we have reached and explored.

When we reach a node, we can check if it is already in \(M\).
If it is, we’ve explored it already and shouldn’t again.

Let’s introduce another set \(Q\) as a queue of nodes which have been reached but not explored.

3.4.2 Algorithm Idea

Initialize \(Q\) as \(Q = \{s\}\). Each iteration:

Choose vertex \(i \in Q\) to explore.
Add to \(Q\) any neighbors of \(i\) that are not already in \(Q\) or \(M\).
Add \(i\) to \(M\) since it has been explored.

If \(Q = \{\} = \emptyset\) (empty set), then stop:

We’ve explored all nodes reachable from \(s\).
\(M\) is the set of nodes reachable from \(s\).

3.4.3 Graph Reachability Algorithm (Pseudocode)

Initialize Q = {s} and M = {}. 

while Q != {}:

    # select a node i in Q
    Q = Q - {i} # remove i from Q.
    
    for j in L(i): # j is adjacent to i.
    
        if (j not in M) and (j not in Q):
            Q = Q + {j} # add j to Q.
            
    M = M + {i} # add i to M.

3.5 Returning to the Example

Let’s consider the graph \(G\) given in Figure 2 (a) and apply the algorithm to find the set of nodes reachable from \(s=1\).

3.5.1 Iteration 1

We initialize \(Q\) and \(M\) as \[ Q = \{1\}, \hspace{0.25in} M = \emptyset. \] Let’s explore node \(1\):

Node 1 has adjacency list \(L(1) = \{2,4\}\).
Let’s add {2,4} to \(Q\).
Since we have explored node \(1\), we remove \(1\) from \(Q\) and add \(1\) to \(M\).