8 Matching Problems

8.1 The Unweighted Matching Problem

8.1.1 Motivation

Given resources and locations, as well as compatibility constraints, we we want to match/assign resources to locations to create as many pairs as possible.

Assignment of workers to jobs, students to internships, etc;
Assign flights to gates;
Assignment of physicians to hospitals, and so on.

8.1.2 Matchings

Definition 8.1 (Matchings) Given an undirected graph $G = (V,E)$ with $n$ nodes and $m$ edges, we call a subset of edges $M \subseteq E$ a matching if it satisfies one of the following equivalent properties:

No two edges in $M$ are incident with the same vertex.
$H = (V, M)$ has node degrees with values $0$ or $1$.

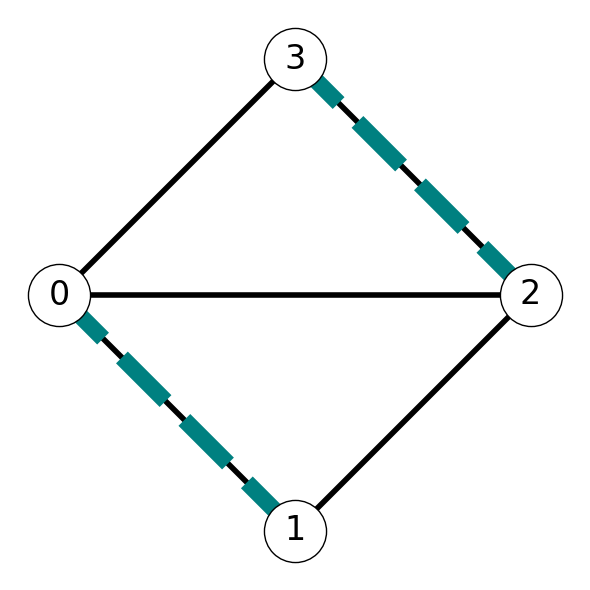
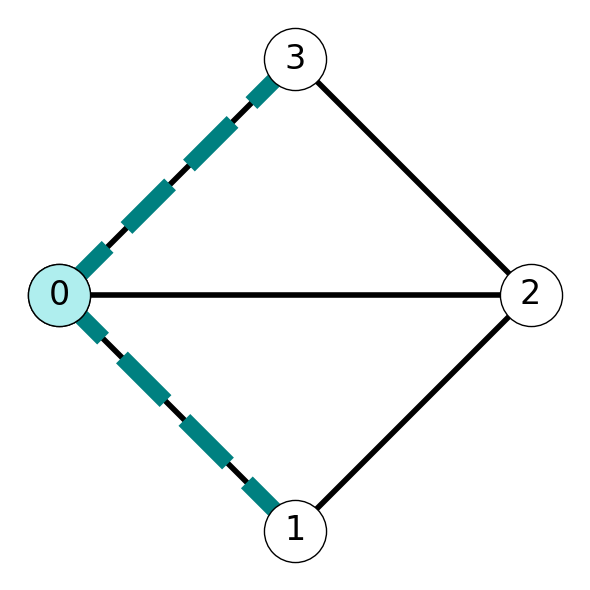
Example 8.1 Consider the graph $G$ given in Figure 8.1. The set $M = \{01, 23\}$ is a matching. On the other hand $\tilde{M} = \{01, 03\}$ is not a matching since it includes two edges incident with $0$.

8.1.3 Bipartite Graphs

We will focus on the task of finding matchings in special class of graphs, namely, bipartite graphs.

Definition 8.2 (Bipartite Graphs) An undirected graph $G = (V,E)$ is bipartite if $V$ can be partitioned into two disjoint sets $A$ and $B$ such that for each $(i,j) \in E$:

Either $i \in A$ and $j \in B$,
Or $j \in A$ and $i \in B$.

We call $A$ and $B$ shores or color classes or independent sets.

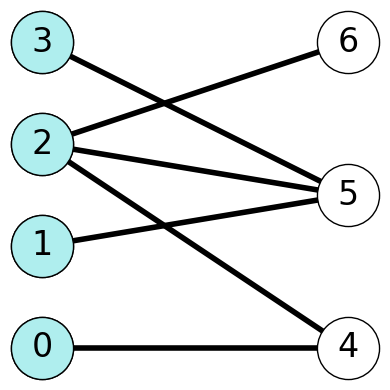
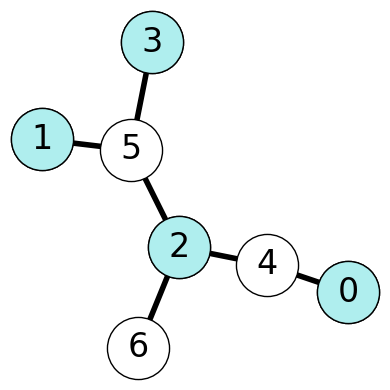
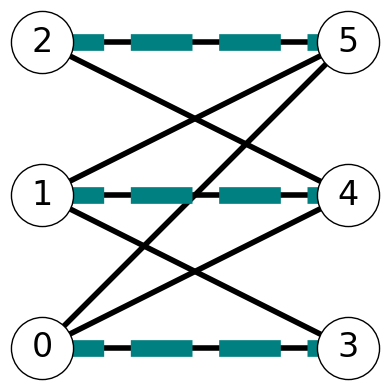
Example 8.2 Figure 8.2 gives two representations of the same bipartite graph $G$. The vertices of $G$ consist of two shores $A = \{0,1,2,3\}$ and $B = \{4,5,6\}$.

8.1.4 The Unweighted Matching Problem

Given a bipartite graph $G$, we want to find the matching of $G$ containing the maximum number of edges.

Definition 8.3 (The Unweighted Matching Problem) Given an undirected graph $G$, find a matching $M \subseteq E$ with maximum cardinality.

Definition 8.4 (The Matching Number) We call the cardinality of a maximum matching the matching number $\nu(G)$.

Example 8.3 The graph given in Figure 8.3 has matching number $\nu(G) = 3$. Indeed, $G$ contains maximum cardinality matchings $M_1 = \{03, 14, 25\}$ and $M_2 = {05, 13, 24}

8.1.5 The Augmenting Path Algorithm

We will construct an algorithm for solving the maximum matching problem, based on construction of augmenting paths. We start by defining a set of nodes that are not incident with matching edges.

8.1.5.1 Exposed Nodes

Definition 8.5 (Exposed nodes) Given a matching $M$, we call any unmatched vertex exposed.

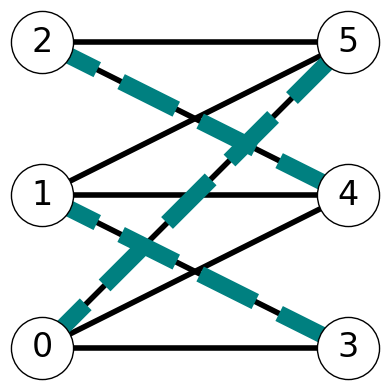
Example 8.4 Consider the matching $M= \{ 05, 24\}$ for graph $G$ given in Figure 8.4. The nodes $1$ and $3$ are exposed for this matching.

8.1.5.2 Alternating Paths and Cycles

Definition 8.6 (Alternating Paths) Given a matching $M$, a path $P$ is an alternating path (cycle) if the edges of the path (cycle) alternate between $M$ and $E \setminus M$.

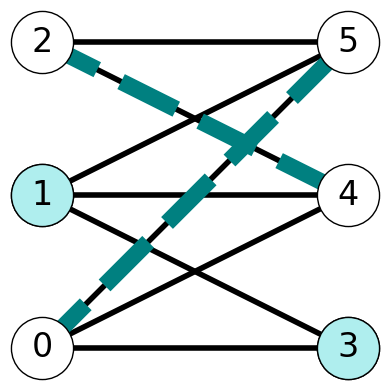
Example 8.5 Consider the graph $G$ with matching $M= \{ 05, 24\}$. Figure 8.5 highlights an alternating path $P=(0,5,2,4)$ and an alternating cycle $C = (0,5,2,4,0)$. We use dashed edges to indicate edges in both $M$ and $P/C$ and dash-dotted edges for edges not in $M$.

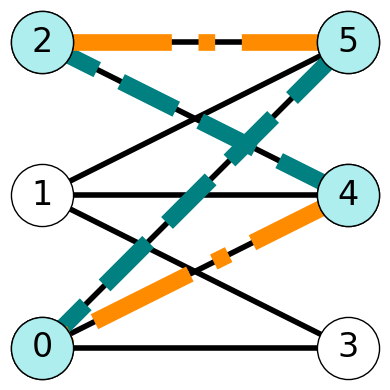
8.1.5.3 Augmenting Paths

We will iteratively identify alternating paths along which to increase the cardinality of a known matching. To do so, we use the following definition of an augmenting path.

Definition 8.7 (Augmenting Path) An alternating path is an augmenting path if it starts and ends with an exposed node.

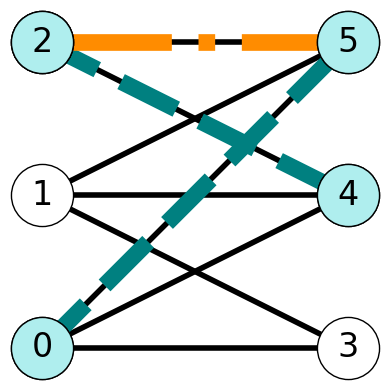
Example 8.6 Consider $G$ with matching $M = \{05, 24\}$ again. Recall that the nodes $1$ and $3$ are exposed. The path $P = (1,5,0,3)$ is an augmenting (1,3)-path Indeed, the edges of this path alternate between edges not in $M$ and those in $M$, and the path starts and ends with exposed nodes.

Figure 8.6: An augmenting path $P=(1,5,0,3)$

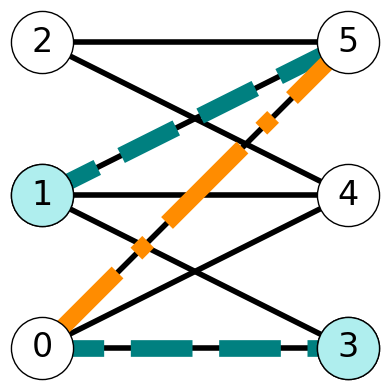
8.1.5.4 Properties of Augmenting Paths

Lemma 8.1 Augmenting paths contain an even number of nodes and odd number of edges.

Proof. Suppose that $P$ is an augmenting path for matching $M$. Since $P$ is augmenting, it starts and ends with an exposed node.

This implies that the first and last edges of $P$ are not in $M$. Consequently, if $P$ contains $k$ edges in $M$, then $P$ must contain $k+1$ edges in $E\setminus M$ since $P$ is an alternating path. Therefore, $P$ contains $2k+1$ edges total, which is odd for every nonnegative integer $k$.

Theorem 8.1 (The Augmenting Path Theorem) A matching $M$ has maximum cardinality if and only if it admits no augmenting paths.

Proof. We start by proving necessity. Suppose that $M$ is a maximum cardinality matching; we want to show that $M$ has not augmenting paths.

We’ll do so by contradiction. Suppose that $M$ has augmenting path $P$. Let’s consider the symmetric difference of $M$ and $P$: \[ \begin{aligned} M' &= M \Delta P &= (M\cup P) \setminus (M\cap P) \\ &= (M \setminus P) \cup (P \setminus M). \end{aligned} \]

Let $P = ((v_1, v_2), (v_2, v_3), \dots, (v_{2k+1}, v_{2k+2}))$; we can assume that $P$ contains an even number of nodes by Lemma 8.1.

We’ll use this fact to construct a matching with more edges than $M$:

We know that $(v_1, v_2) \notin M$ since $v_1$ is exposed. This implies that $(v_1, v_2) \in M'$.
Next, $(v_2, v_3)$ is in $M\cap P$ because $P$ is an alternating path. Therefore, $(v_2, v_3) \notin M'$.

We can continue this pattern to establish that $M'$ is a matching. If $P$ contains $k$ edges in $M$ and $k+1$ edges in $E\setminus M$, then $M'$ must consist of the $k+1$ edges in $E\setminus M$. This implies that $M$ is not a maximum matching; a contradiction. Therefore, if $M$ is a maximum matching then no augmenting path exists.

Let’s now prove sufficiency. Suppose that there is no augmenting path. Let’s assume that $M$ is not a maximum matching and find a contradiction.

By assumption, there is some matching $M'$ with $|M'| > |M|$. Let’s consider the symmetric difference \[ M'' = M \Delta M' = (M\setminus M') \cup (M' \setminus M). \]

Let’s consider three subgraphs of $G$:

$H = (V, M)$;
$H' = (V, M')$; and
$H'' = (V, M'')$.

Figure 8.7 gives an example illustrating the construction of these three subgraphs.

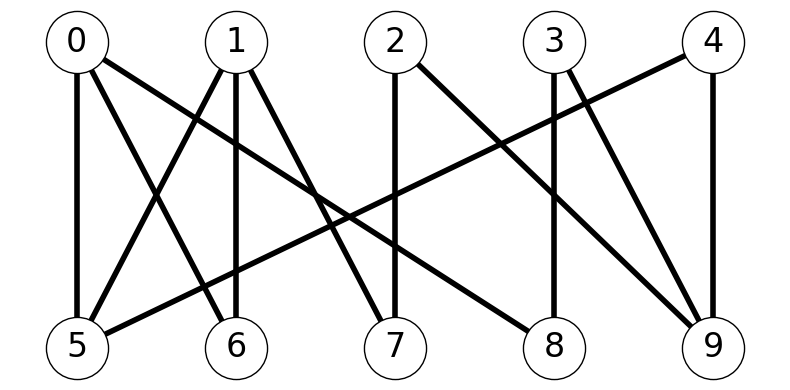
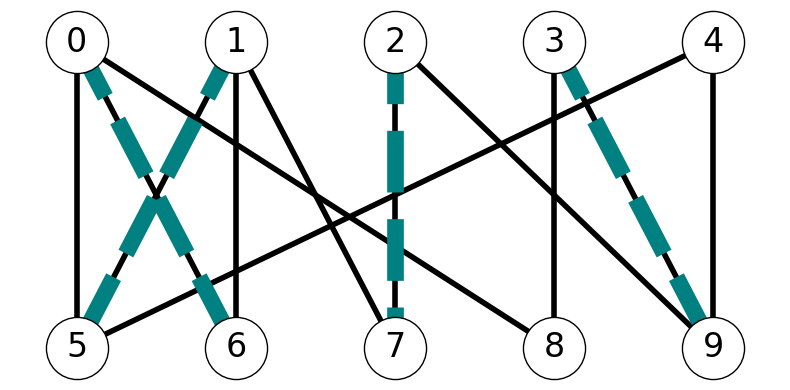
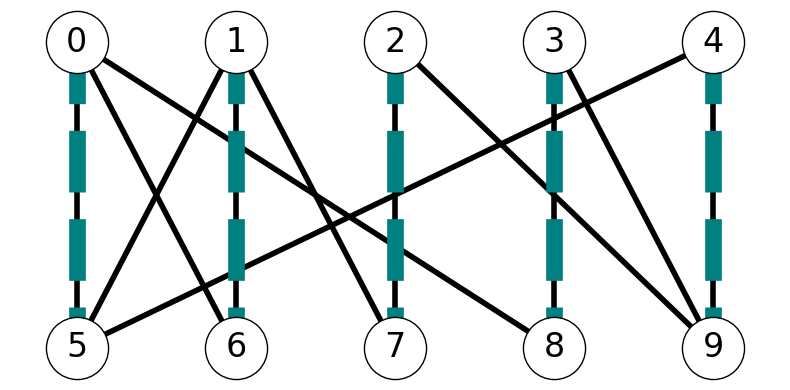
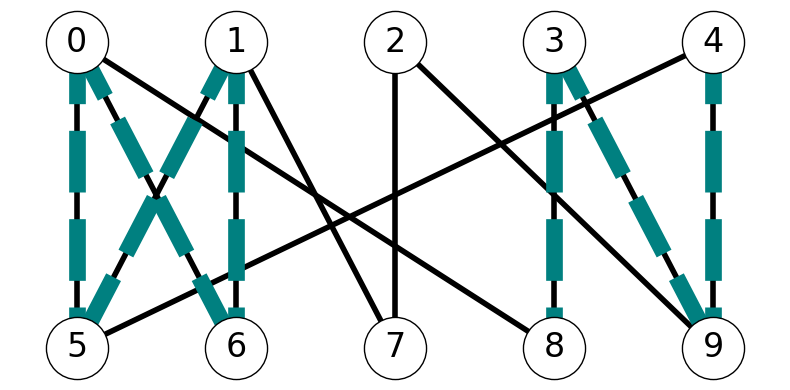
Let’s consider maximally connected subgraphs of $H''$; these are subgraphs that adding an node creates a disconnected subgraph of $G$. Note that:

Nodes in $H$ and $H'$ have either degree $0$ or $1$, since $H$ and $H'$ are both induced by matchings.
This implies that the nodes in $H''$ have degrees in $\{0,1,2\}$.

Therefore, each maximally connected component of $H''$ is one of:

an isolated node;
an alternating path; or
an alternating cycle.

Since $|M'| > |M|$ there is some maximally connected subgraph $C$ with more edges from $M'$ than edges from $M$. Note that $C$ is not an isolated node. Moreover, $C$ is not an alternating cycle, because an alternating cycle would contain the same number of edges from $M$ and $M'$. Therefore, $C$ is an alternating path. Further, $C$ is an augmenting path. Indeed, Its end points are exposed with respect to $M$, since it is alternating and contains more edges from $M'$ than $M$.

8.1.6 The Augmenting Path Algorithm

While augmenting path $P$ exists:

Find an augmenting path $P$
If $P \neq \emptyset$:
- $M \gets \left( M \cup P\right) \setminus \left(M \cap P \right).$
Else:
- STOP (exit loop).

8.1.7 Finding an Augmenting Path

We need an algorithmic way to identify an augmenting path. To do so, we will work with an auxiliary graph.

8.1.7.1 The Auxiliary Graph

We build an auxiliary directed bipartite graph $G' = (V, E')$ where, for each $\{i,j\} \in E$, $i \in A$, $j\in B$:

Add $(i,j)$ to $E'$ if $\{i,j\} \notin M$.
Add $(j,i)$ to $E'$ if $\{i,j\} \in M$.

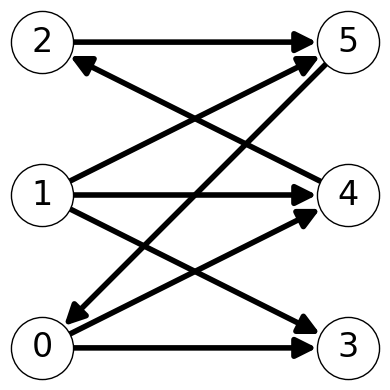
The vertex set $A$ can be left only via arcs corresponding to edges not in $M$.

The vertex set $B$ can only be left via arcs corresponding to edges in $M$.

This implies that paths in $G'$ are alternating.

Paths between exposed nodes $i \in A$ and $j \in B$ are augmenting.

8.1.7.2 A Practical Algorithm for Finding an Augmenting Path

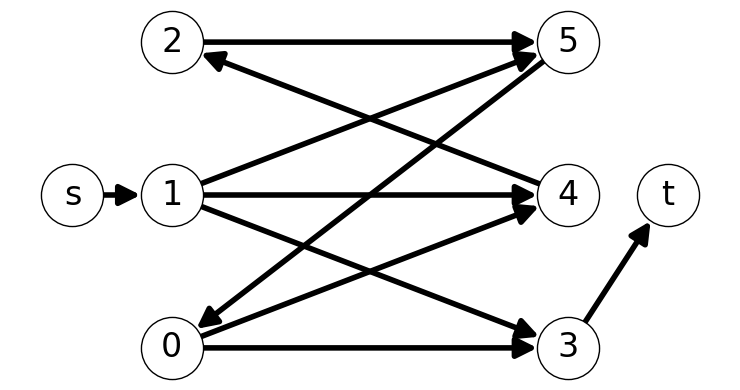
To find an augmenting path using $G'$:

Introduce two extra nodes $s,t$.
Connect $s$ to all the exposed nodes in $A$.
Connect $t$ to each exposed node in $G$.
Look for an $st$-path in the extended version of $G'$.

Example 8.7 Figure 8.9 illustrates the construction of the extended auxiliary graph with graph $G$ containing matching $M = \{05, 24\}$.

(a) Graph $G$ with matching $M = \{05, 24\}$

8.1.8 Complexity of the Augmenting Path Algorithm

8.1.8.1 Operations per Iteration

To find an augmenting path $P$ costs $O(m+n)$. Indeed, we need to construct the auxiliary graph and then apply a variant of graph reachability to find an $st$-path in the auxiliary; both steps cost $O(m+n)$ elementary operations.

On the other hand, updating $M$ as $M \Delta P$ costs $O(n)$ operations.

Therefore, the total complexity is \[ \text{maximum \# of iterations } \times O(m + n). \]

8.1.8.2 Total Number of Iterations

Notat that a matching $M$ has at most $n/2$ edges in a bipartite graph. Indeed, \[ \nu(G) \le \min \{|A|, |B|\} \le \frac{n}{2}. \] The augmenting path algorithm increases the cardinality of a matching by $1$ each iteration. Therefore, the augmenting path algorithm has total complexity bounded above by \[ O\Big( \nu(G) \times (m+n)\Big) = O( n^2 + mn). \] If $G$ is connected, we have $n \le m+1 = O(m)$. In this case, we have total complexity $O(mn)$.

8.1.9 Example

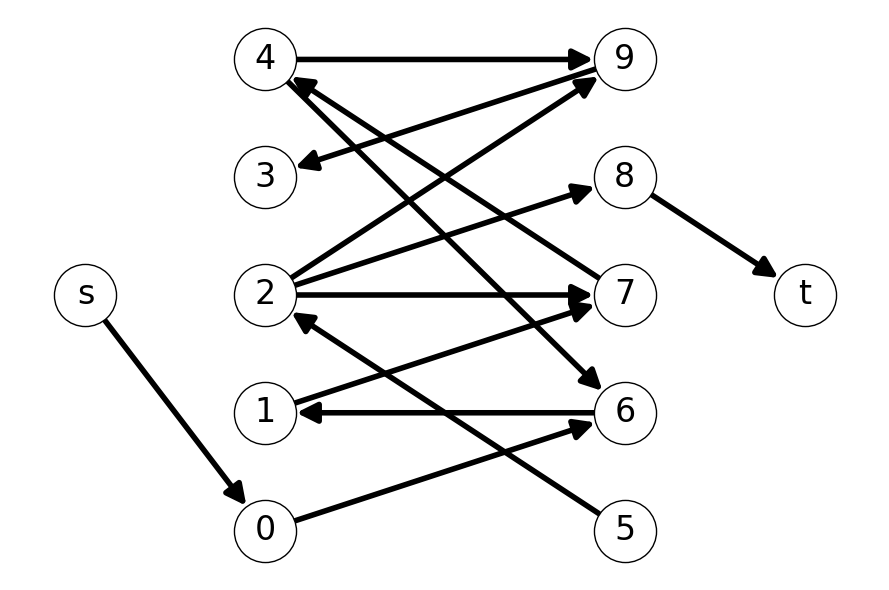
Example 8.8 Consider the graph $G$ given in Figure 8.10 with initial matching \[ M_0 = \{16, 27, 39\}. \]

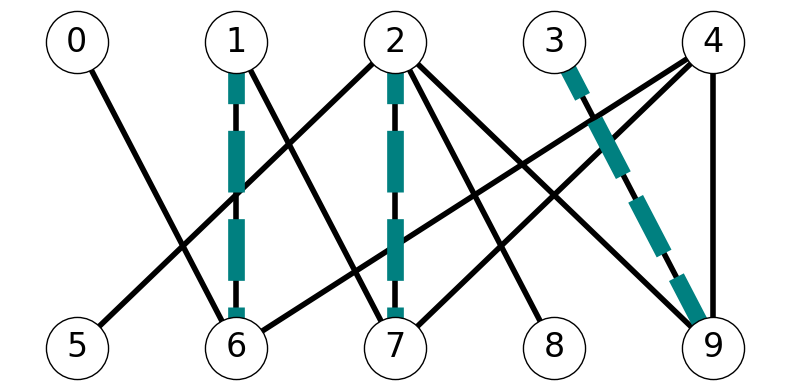
Figure 8.10: Graph $G$ for Example 8.8 with matching $M_0$.

8.1.9.1 Step 1

We start by constructing the auxiliary graph $G'$. After doing so, we can observe that there is an $st$-path $P' = (s,4,7,2,5,t)$ in $G'$. This gives the augmenting path $P = (4,7,2,5)$.

We update the matching \[ M_1 = M_0 \Delta P = (M_0 \cup P) \setminus (M_0 \cap P) = \{16, 39, 25, 47\}. \]

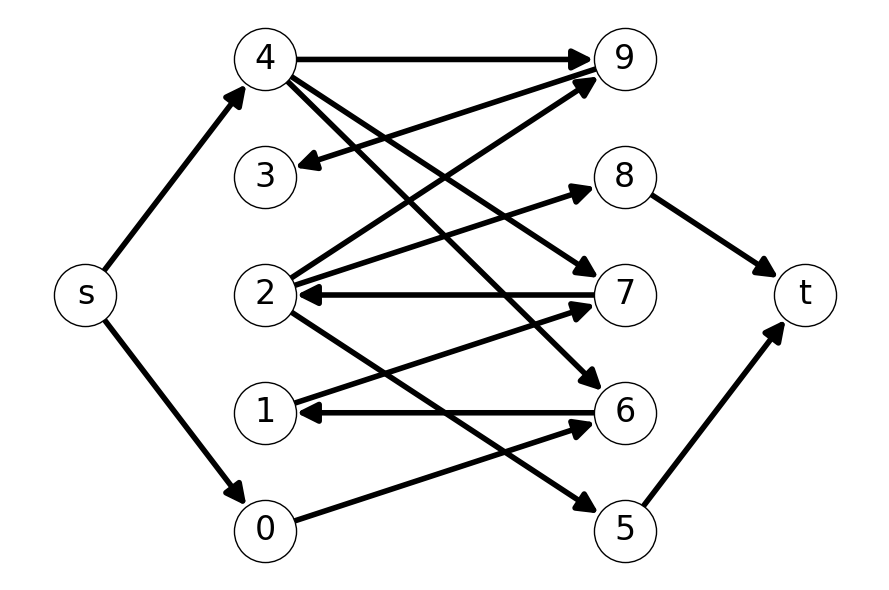
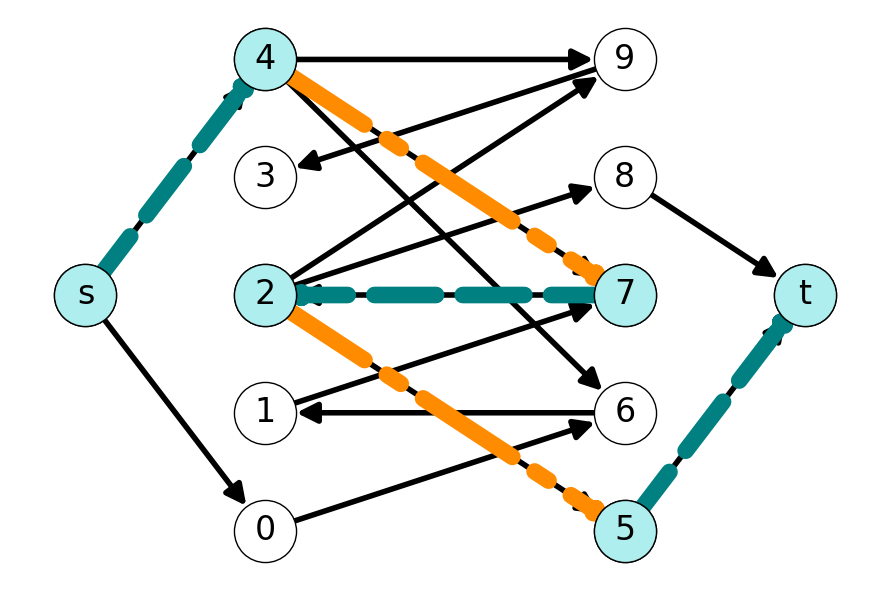
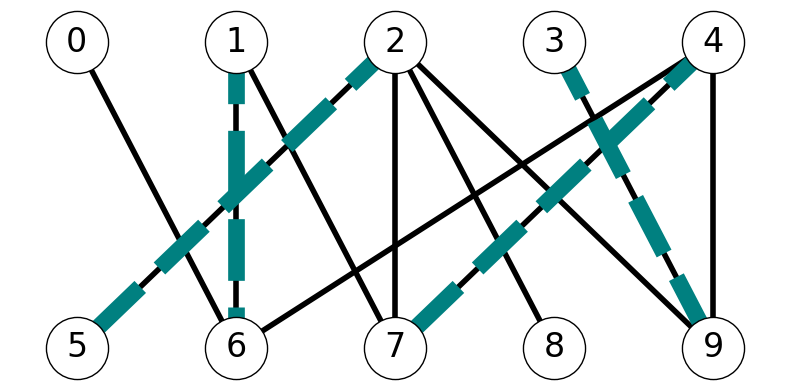
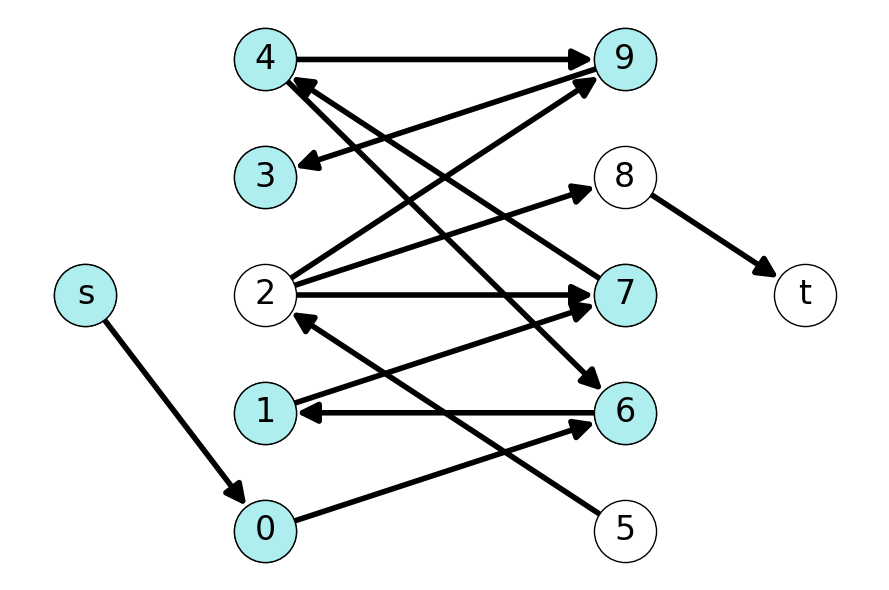
8.1.9.2 Step 2

As before, we construct the auxiliary graph $G'$ (Figure 8.12 (a)). Note that $t$ is not reachable from $s$ in $G'$; Figure 8.12 (b) gives the reachable set from $s$ in $G'$.

This implies that there are no augmenting paths for matching $M_1$. Therefore, $M_1$ is a maximum matching.

8.2 The Weighted Matching Problem

8.2.1 Problem Definition

Definition 8.8 (Weighted Matching Problem) Given an undirected graph $G = (V,E)$ and a weight function $w: E \mapsto \mathbf{R}$, find a matching $M \subseteq E$ of maximum weight: \[ w(M) = \sum_{\{i,j\} \in M} w_{ij}. \]

Definition 8.9 (Weighted Matching Number) We call the weight of a maximum-weight matching of $G$ the weighted matching number and denote it $\nu_w(G)$.

8.2.2 Extremality

Definition 8.10 (Extreme Matchings) We call a matching extreme if it has maximum weight among all matchings of the same cardinality $|M|$.

Question: We know how to construct another matching of cardinality one unit larger using the unweighted matching algorithm.

Can we construct this matching so that it is extreme?
If so, we can build an extreme matching $M_1$ from an empty matching $M_0$. From $M_1$, we can build an extreme matching $M_2$ of size $2$, and so on.

8.2.2.1 An Observation

Theorem 8.2 If $M_1, M_2, \dots, M_{\nu(G)}$ is a sequence of extreme matchings of increasing size, then \[ M = \textrm{arg max} \Big\{ w(M_i): i = 1, 2, \dots, \nu(G) \Big\} \] is a maximum-weight matching.

Here, the $\textrm{argmax}$ operator returns a extreme matching with maximum weight:

if a maximum weight matching has cardinality $1$, then $M_1$ is a maximum weight matching;
if a maximum weight matching has cardinality $2$, then $M_2$ is a maximum weight matching; etc.

8.2.3 Augmentation and Weights of Matchings

Let $M$ be a matching and let be $P$ an augmenting path.

Let \[ M' := M \Delta P = (M \cup P) \setminus (M\cap P) = (M\setminus P) \cup (P \setminus M). \] The weight of $M'$ is \[ w(M') = \sum_{ij \in M'} w_{ij} = w(M) + \underbrace{ \sum_{e \in P\setminus M} w_i - \sum_{e \in P \cap M} w_e}_{=:(*)}. \] The summand $(*)$ is a linear combination of weights of edges in $P$ with

coefficient $+1$ if $e \notin M$;
coefficient $-1$ if $e \in M$.

Let’s introduce new weights and rewrite the identity: \[ \ell_{ij} = \begin{cases} -w_{ij} & \text{if } ij \notin M, \\ + w_{ij} & \text{if } ij \in M. \end{cases} \] Using these lengths, we have \[ w(M') = w(M) - \sum_{ij \in P} \ell_{ij}. \] This implies that the increase in weight is maximized if the length of $P$ is minimized.

8.2.4 The Shortest Augmenting Path Theorem

Question: Suppose that we augment an extreme matching $M$ by a shortest augmenting path.

Does this yield an extreme matching $M'$ (with cardinality $|M'| = |M| + 1$)?

We have the following theorem.

Theorem 8.3 Given an extreme matching $M$ and an augmenting path $P$ of minimum length.

The matching $M' := M \Delta P$ is an extreme matching of cardinality $|M'| = |M| + 1$.

Proof. We’ll use contradiction. Let’s assume that $M'$ is not extreme. Then there is $N'$ with $|N'| = |M'|$ such that \[ w(N') > w(M'). \] We know that $|N'| = |M'| > |M|$. By an identical argument to the proof in the unweighted case, the subgraph \[ G_{M \Delta N'} = (V, M \Delta N') \] has a maximal connected component $C$ with maximal connected component $C$ with more edges from $N'$ than $M$, i.e., an alternating path. This alternating path augments $M$. (Notes $C$ may not be $P$.)

Earlier, in the unweighted case, we used $C$ to extend $M$ to a larger matching. Here, we’ll do the opposite: we’ll shrink $N'$ using $C$: \[ N = N' \Delta C. \] Note that \[ |N| = |N'| - 1 = |M|. \] We have

four matchings $M, N, M', N'$;
two augmenting paths $P$ and $C$.

By assumption $\ell(P) \le \ell(C)$. Moreover, $w(M) \ge w(N)$. It follows that \[ w(M') < w(N') = w(N) - \ell(C) \le w(M) - \ell(P) = w(M'). \] This is a contradiction. Therefore, $M'$ is an extreme matching.

8.2.5 The Iterative Shortest Path Algorithm

8.2.5.1 The Algorithm

Initialize $M_0 = \emptyset$.

For $i=0,1,2,\dots, \nu(G)$:

Find a shortest $M_i$-augmenting path $P$.
If $P \neq \emptyset$:
- $M_{i+1} \gets \left( M_i \cup P\right) \setminus \left(M_i \cap P \right).$
- $w(M_{i+1}) \gets w(M_i) - \ell(P)$
Else:
- STOP (exit loop).

Return $M = \textrm{arg max} \{w(M_i)\}$.

8.2.5.2 Finding a Shortest Augmenting Path

We need to find augmenting paths. To do so, we construct an auxiliary graph and identify the shortest path, which will yield the desired augmenting path.

Build an auxiliary directed graph $G' = (V \cup \{s,t\}, A')$ for matching $M_i$:
For each $\{i,j\} \in E$:
- Add $(i,j)$ to $A'$ if $\{i,j\} \notin M_i$ with length $\ell_{ij} = - w_{ij}$.
- Add $(j,i)$ to $A'$ if $\{i,j\} \in M_i$ with length $\ell_{ij} = w_{ij}$
Connect $s$ and $t$ to/from the exposed nodes in the two shores with zero length arcs.
Finally, find a shortest $st$-path in $G'$.

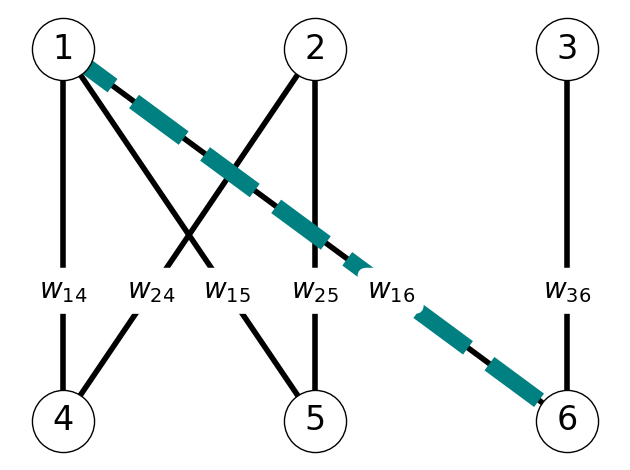
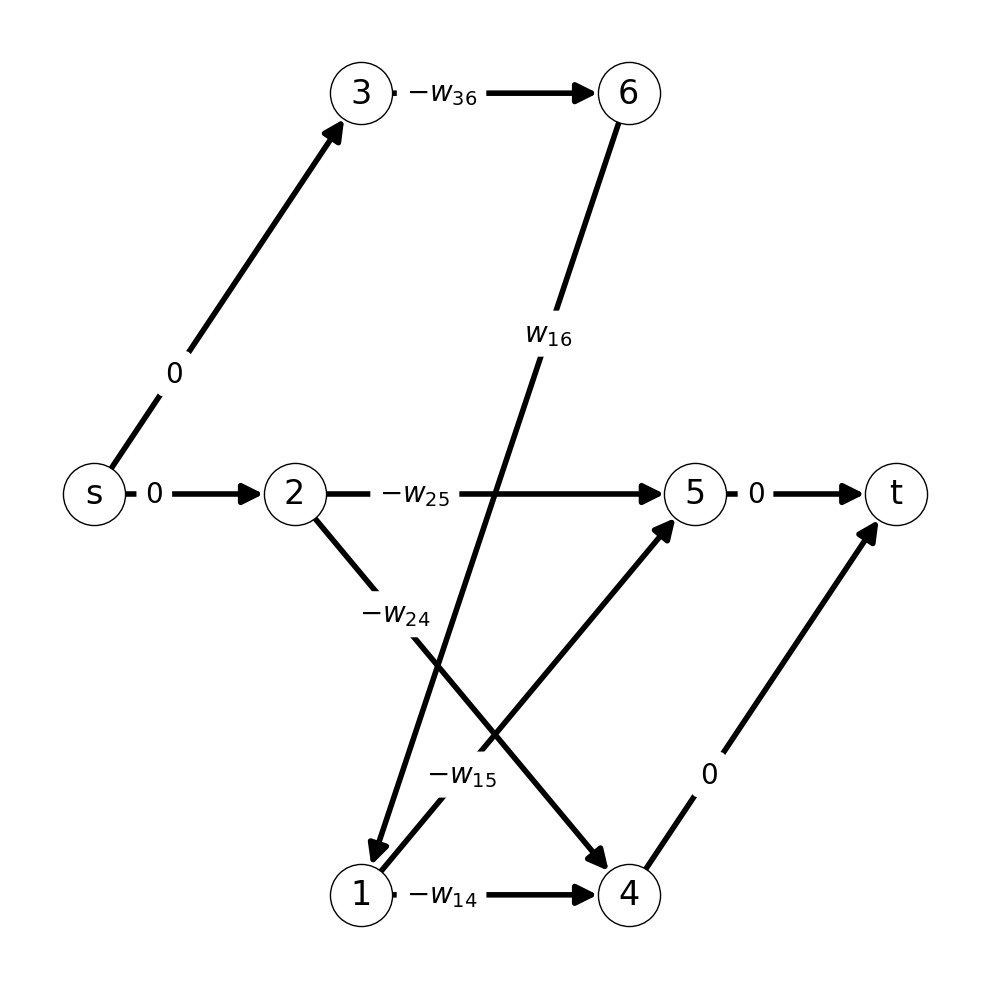
Example 8.9 Figure 8.13 illustrates the construction of the auxiliary graph for a given matching $M_0$.

8.2.5.3 Cycles in Bipartite Graphs

Question: The auxiliary graph $G'$ has edges with negative lengths.

Is it possible to have cycle with negative length?
In this case, the shortest-path problem is ill-posed.

We will use the following lemma to address this possible issue.

Lemma 8.2 Every directed bipartite graph $G$ does not contain odd cycles

Proof. We use contradiction. Let’s assume that $G$ has a cycle $C$ with odd length. Specifically, assume $C$ has $2k+1$ nodes for some positive integer $k$; label these nodes as $v_1, v_2, \dots, v_{2k+1}$.

Since $G$ is bipartite, we change shore with each edge. That is, $v_i, v_{i+1}$ are in different shores. The last edge in the cycle is $(v_{2k+1}, v_1)$. Since $C$ has odd length, $v_1$ and $v_{2k+1}$ are in the same shore of $G$. Thus, this edge cannot exist; a contradiction.

Therefore, any cycle in $G$ has even length.

The following theorem confirms that the auxiliary graph does not have negative-length cycles if the matching $M$ is extreme.

Theorem 8.4 If $M$ is an extreme matching then $G'$does not contain negative-length cycles.

Proof. To obtain a contradiction, suppose $C$ is a cycle with negative length: \[ \ell(C) = \sum_{e \in C} \ell_e < 0. \] Since $G'$ is bipartite, $C$ has even length by Lemma 8.2. Moreover, $C$ is alternating by the orientation of arcs of $G'$.

Now, consider $M' = M \Delta C$. Note that \[ |M'| = |M|. \] Indeed, $C$ is even so half of the edges in $M\cup C$ are in $M\cap C$. Thus, \[ |C| = |M| + |M'| \] is even and $|M| = |M'|$..

Now consider the weight of $M'$: \[ w(M') = w(M) - \ell(C) > w(M) \] since $\ell(C) < 0$. Therefore, $M$ is not an extreme matching.

8.2.6 Complexity

For each $i = 0, 1, 2, \dots, \nu(G)$, we need $O(n+m)$ operations to form the auxiliary graph $G'$ and $O(nm)$ operations to find the shortest $st$-path using the Bellman-Ford Algorithm. After identifying a shortest $M_i$-augmenting path, we need a further $O(n)$ operations to compute $M_{i+1}$. Thus, each iteration has complexity $O(mn)$.

We repeat this process $\nu(G) = O(n)$. Thus, the total complexity is \[ O(\nu(G) mn) = O(n^2 m). \]

8.2.7 Example

Example 8.10 Consider the graph $G$ given in Figure 8.14.

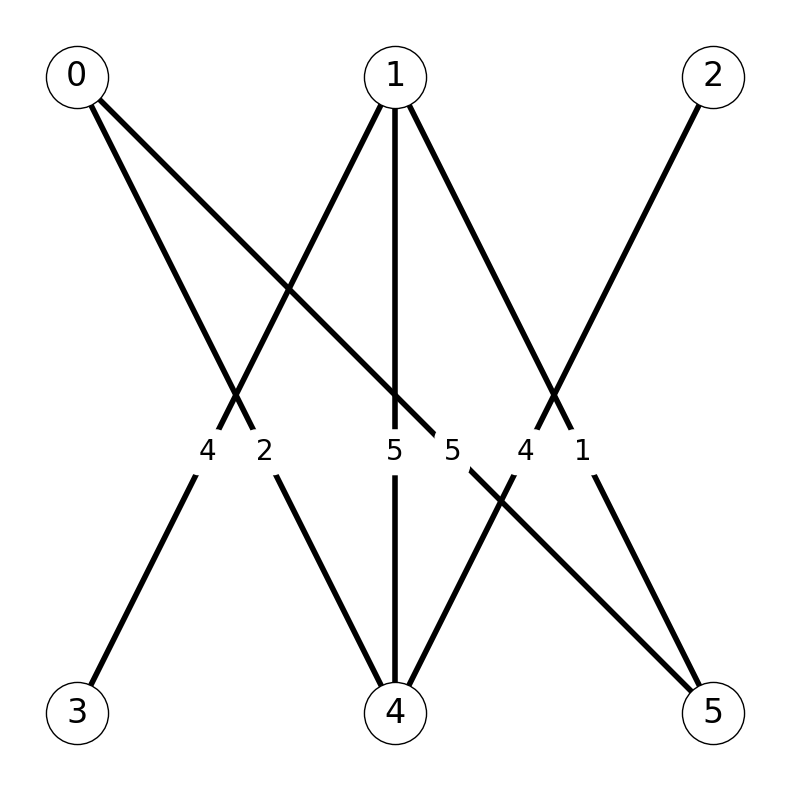
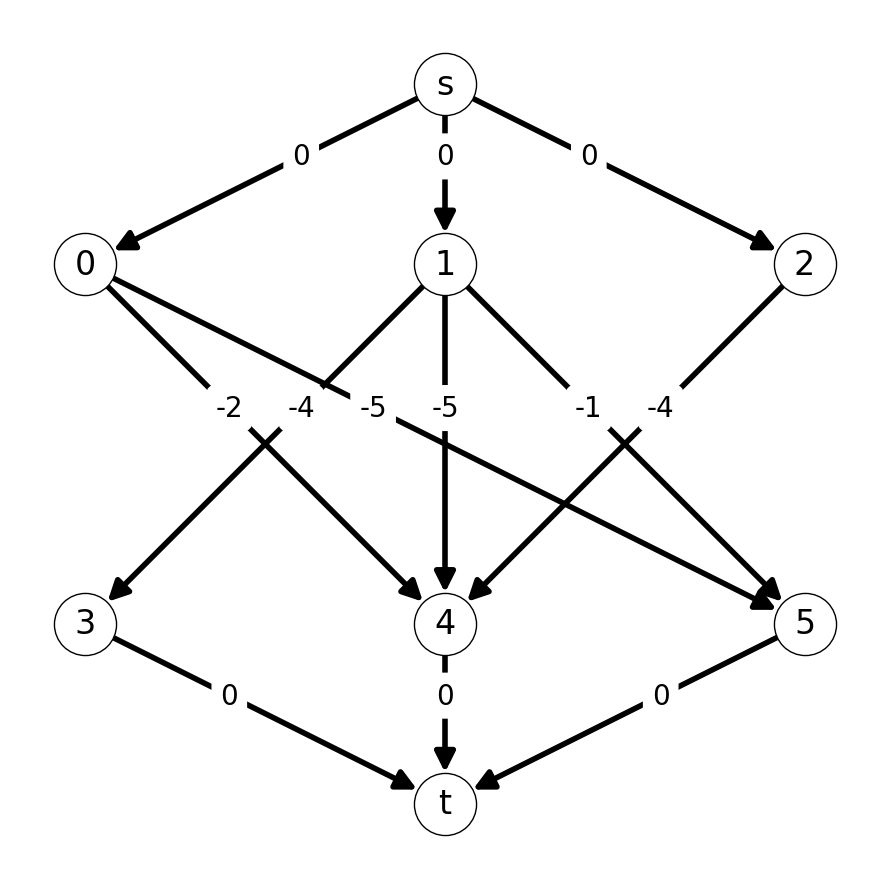
Step 1

We start by finding the shortest $st$-path in $G'$. Here, $(s,1,4,t)$ and $(s,0,5,t)$ are both shortest $st$-paths (with length $-5$). We can use either as an augmenting path. Let’s choose $(s,1,4,t)$ to use as an augmenting path and add $14$ to $M_0$ to get $M_1:$ \[ M_1 = M_0 \Delta P_0 = \emptyset \Delta \{14\} = \{14\}; \;\;\; w(M_1) = 5. \]

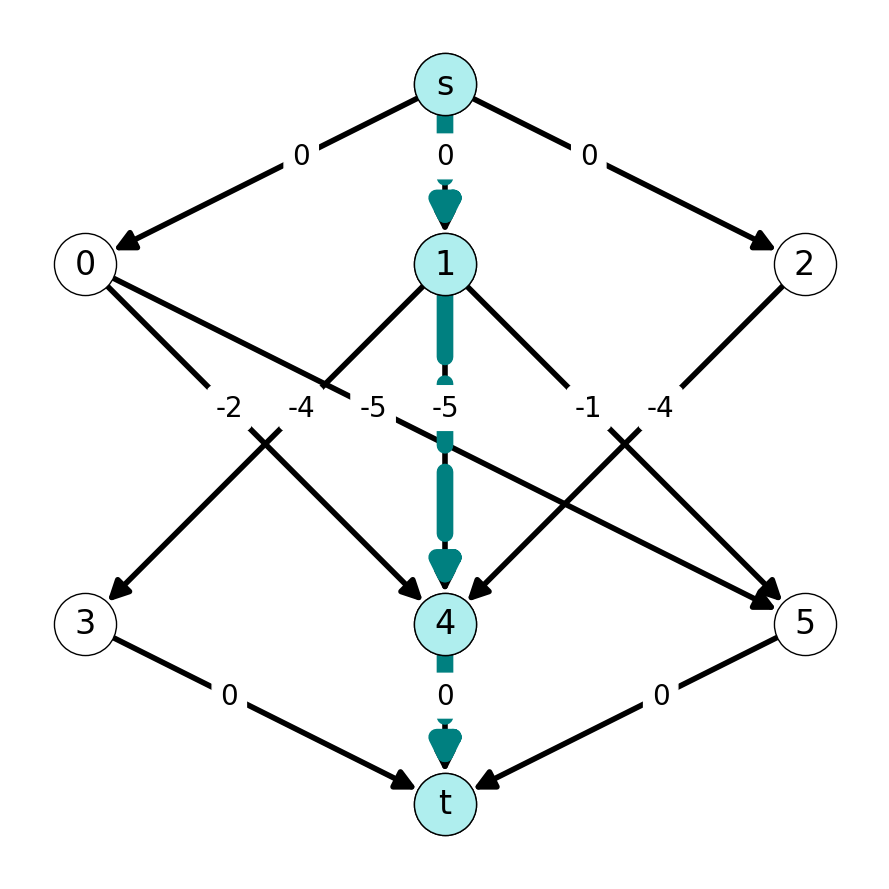
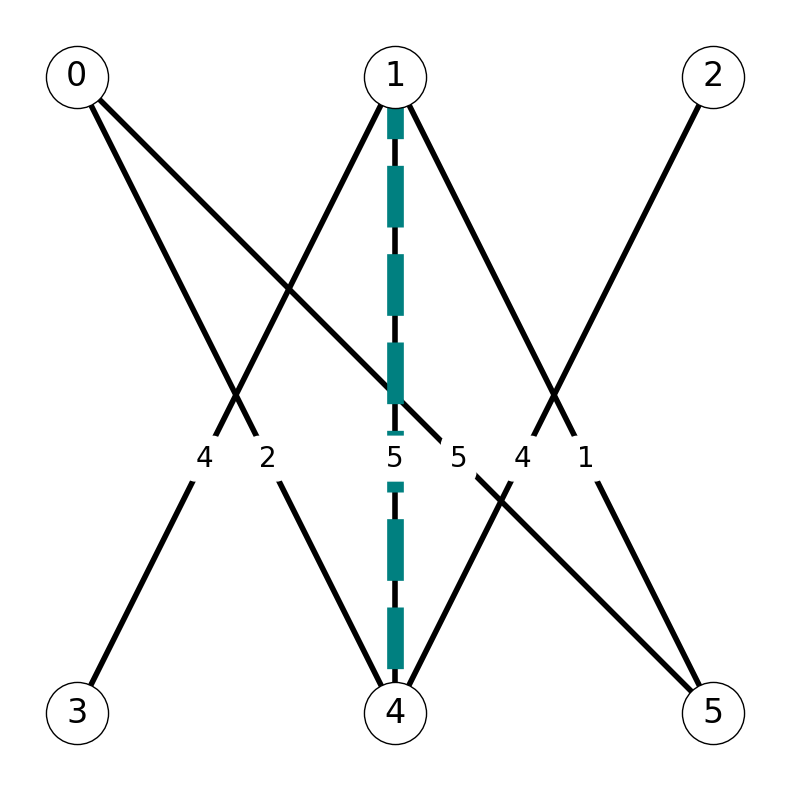
Step 2

The shortest $st$-path in the auxiliary graph $G'$ is $(s,0,5,t)$. We use the path $P_1 = \{05\}$ to update the matching: \[ M_2 = M_1 \Delta P_1 = \{14, 05\}; \;\;\; w(M_2) = 10. \]

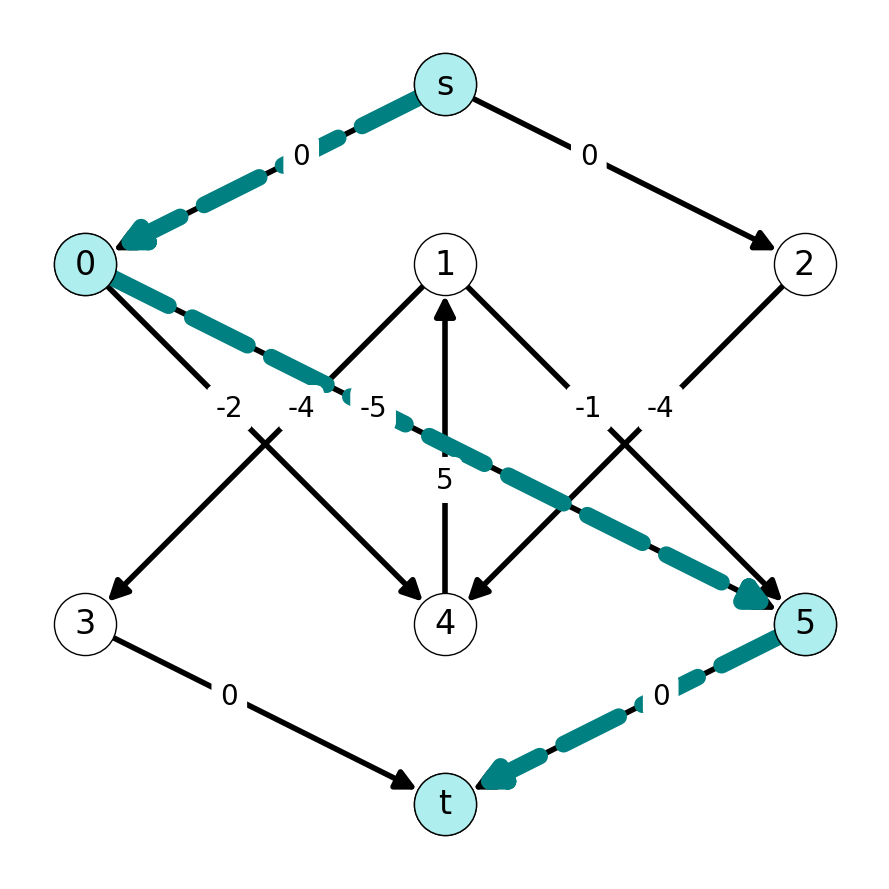
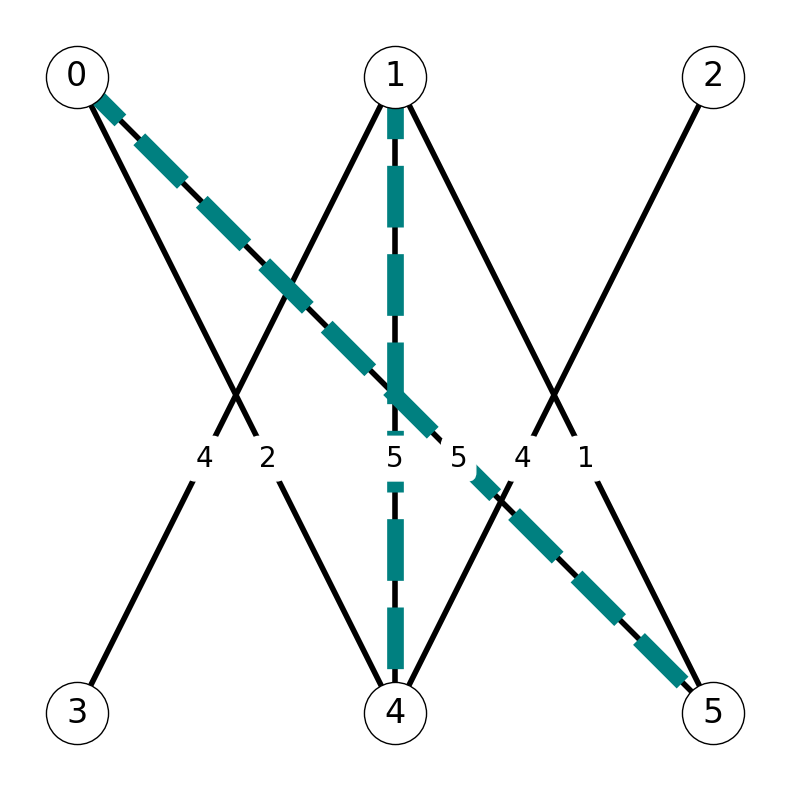
Step 3

Next, the shortest $st$-path is $(s,2,4,1,3,t)$. We compute $M_3$ using $P_2 = (2,4,1,3)$: \[ M_3 = M_2 \Delta P_2 = \{05, 24, 13\}; \;\;\; w(M_3) = 13. \]

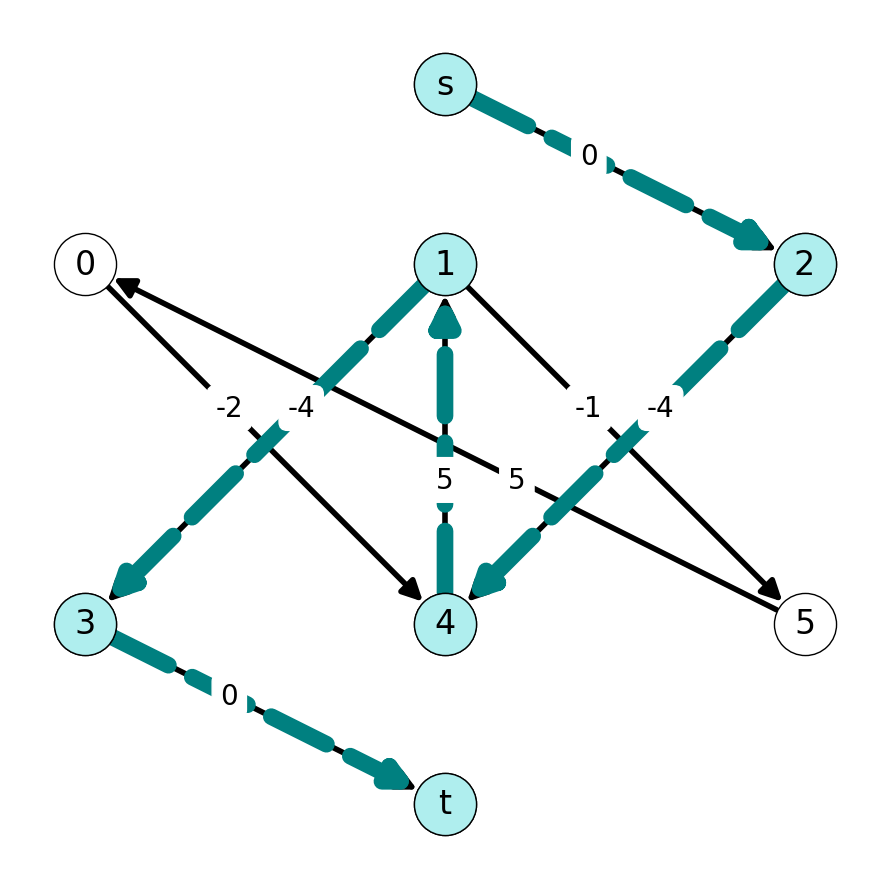
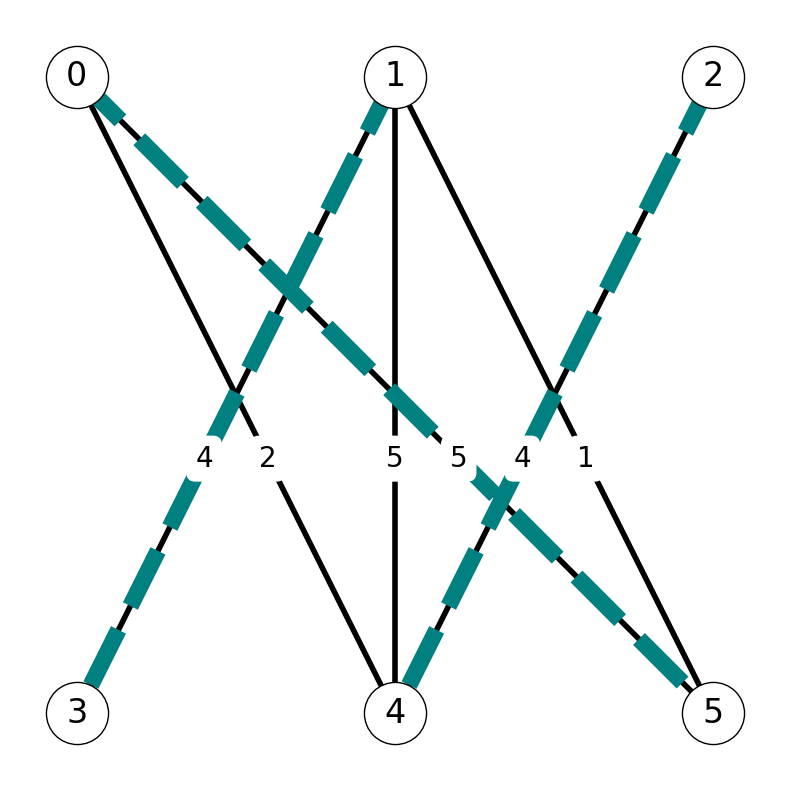
Termination

Each shore has three nodes and we have found a matching with three edges. This implies that the unweighted matching number is $\nu(G) = 3$. We can stop the algorithm.

Note that \[ w(M_3) = 13 = \max\{w(M_0), w(M_1), w(M_2), w(M_3)\}. \] Therefore, $M_3$ is the maximum weight matching.

8.2.8 A Final Remark

The extreme matching of maximum cardinality $M_\nu(G)$ is not necessarily the maximum weight matching!

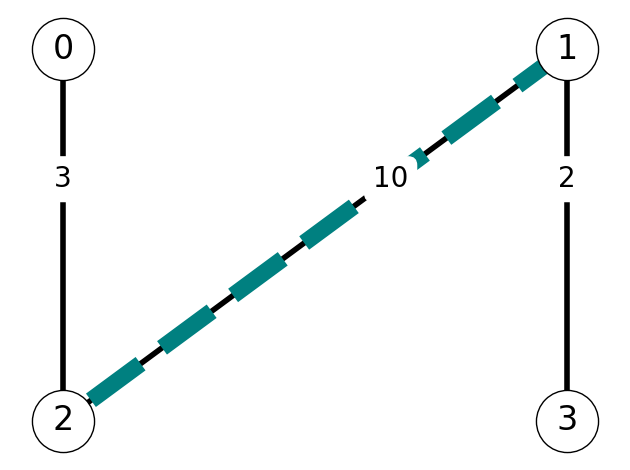
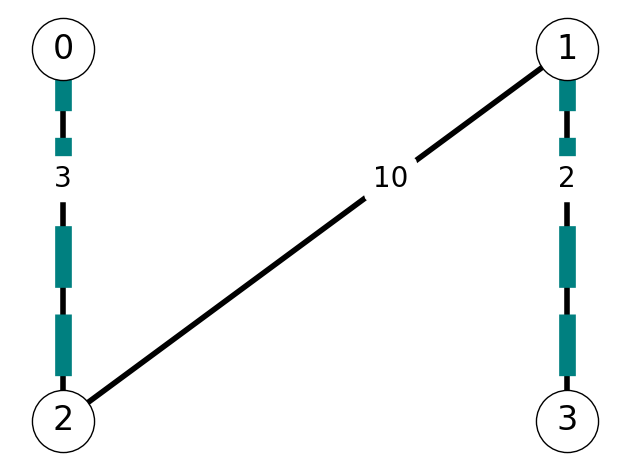
Example 8.11 Consider the graph given in Figure 8.18. This graph has maximum weight matching $M_1 = \{12\}$ and maximum cardinality matching $M_2 = \{02, 13\}$.

8.3 The Assignment Problem

8.3.1 Preliminaries

Definition 8.11 (The Assignment Problem) Given two groups with $k$ items each and a pairwise cost $a_{ij}$ for each $i,j = 1,2,\dots, k$, the assigment problem seeks an assignment of the objects from the first group to the second such that:

Each object is assigned from group 1 to exactly one item in group 2.
The total assignment cost is minimized.

8.3.1.1 Permutations

A permutation is a bijective function $\pi$ mapping $\{1,2,\dots, k\}$ onto itself.

The assignment problem can be expressed in terms of permutations:

Given a $k\times k$ matrix $A$, find a permutation $\pi$ of $\{1,2,\dots, k\}$ maximizing \[ \sum_{i=1}^k a_{i, \pi(i)}. \]

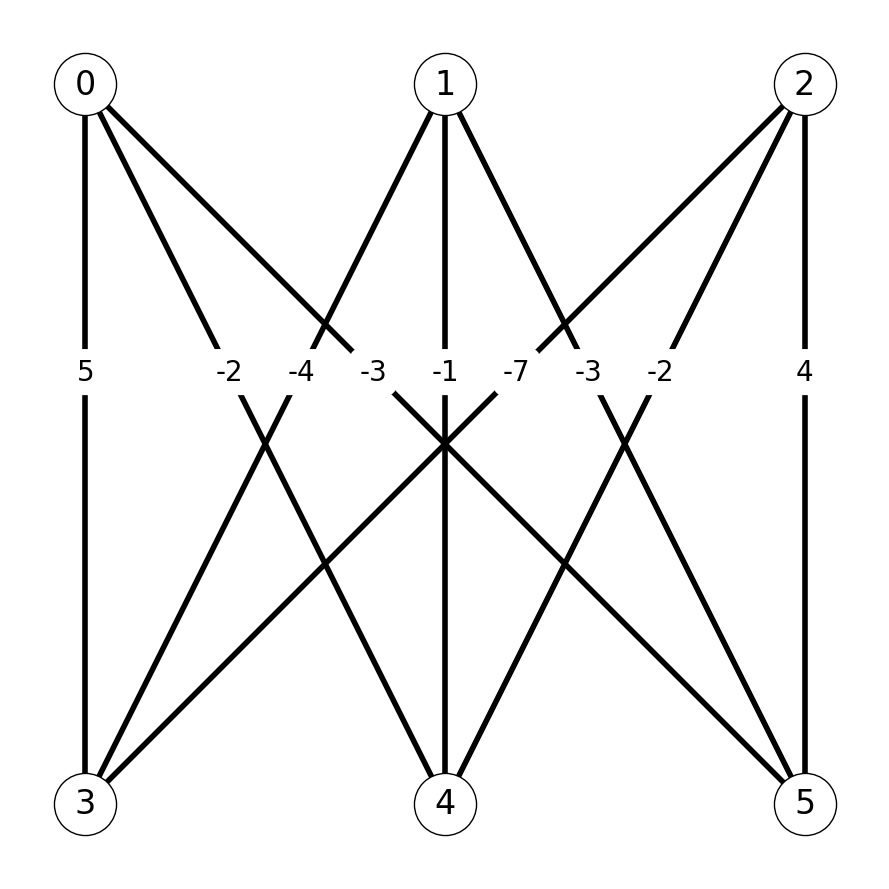
Example 8.12 Suppose $k = 3$ and consider the permutation $\pi$ and pairwise costs $A$ given by \[ \pi(1) = 3, \; \pi(2) = 1, \; \pi(3) = 2, \hspace{0.25in} A = \begin{pmatrix} -5 & 2 & 3 \\ 4 & 1 & 3 \\ 7 & 2 & -4 \end{pmatrix}. \] Then the cost of the assignment according to $\pi$ is \[ a_{1, \pi(1)} + a_{2, \pi(2)} + a_{3,\pi(3)} = a_{13} + a_{21} + a_{32} = 3 + 4 + 2 = 9. \]

8.3.2 Connection to Maximum Matchings

We can cast an instance of the assignment problem as an instance of maximum weighted matching problem:

Construct complete bipartite graph $G = (U \cup V, E)$ with \[ U = \{1,\dots, k\}, \hspace{0.5in} V = \{1', \dots, k'\}. \]
Reverse signs of costs $w_{ij} = -a_{ij}$ to obtain a maximization problem.
Impose constraint $|M| = v(G) = n/2 = k$ to ensure assignment of all objects.

It suffices to apply the augmenting path algorithm for the maximum weighted matching problem with one change:

The minimum cost assignment is the last matching $M_{\nu(G)}$.
This ensures that the assignment constraint is met.

8.3.3 Complexity of the Assignment Problem

We can solve the weighted matching problem using $O(n^2 m)$ EOs using the augmenting path algorithm.

Question: How does this translate to an instance size of the assignment problem?

Let $n$ is the number of vertices $G$ in the bipartite representation of the assignment problem with $k$ nodes in each shore $U$ and $V$: \[ n = |U| + |V| = k + k = 2. \]
$G$ is complete bipartite, so it has \[ k^2 = |U| \times |V| \] edges.

This implies that we need \[ O(n^2 m) = O(k^4) \] elementary operations to solve the assignment problem. This is quadratic in the number, $k^2$, of pairwise assignment costs. Thus, the modified augmenting path algorithm solves the assignment problem using at most a polynomial of its instance size operations.

8.3.4 Example

Example 8.13 Let’s solve the instance of the assignment problem given by cost matrix \[ A = \begin{pmatrix} -5 & 2 & 3 \\ 4 & 1 & 3 \\ 7 & 2 & -4 \end{pmatrix}. \]

Initialization

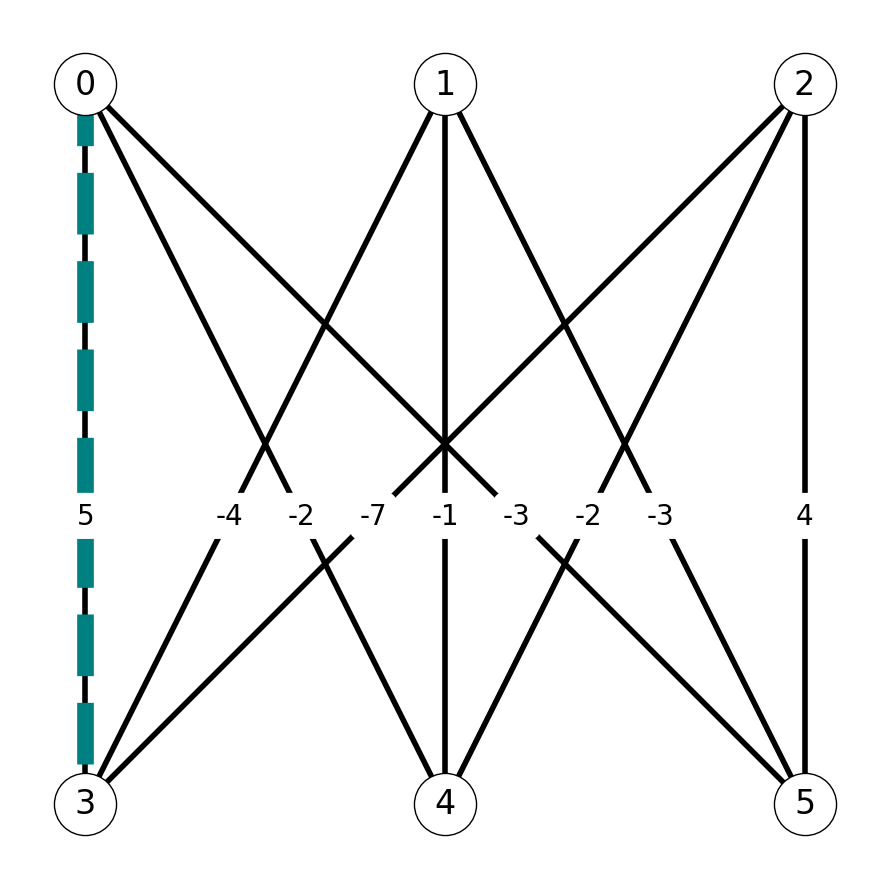
We start by constructing the weight matrix $W$ and constructing the corresponding instance of the maximum weighted matching problem: \[ W = - A = \begin{pmatrix} +5 & -2 & -3 \\ -4 & -1 & -3 \\ -7 & -2 & +4 \end{pmatrix}. \] Associating rows in $A$ and $W$ with nodes $0,1,2$ and columns $3,4,5$ yields an instance of the maximum weight matching problem corresponding to the graph $G$ in Figure 8.19.

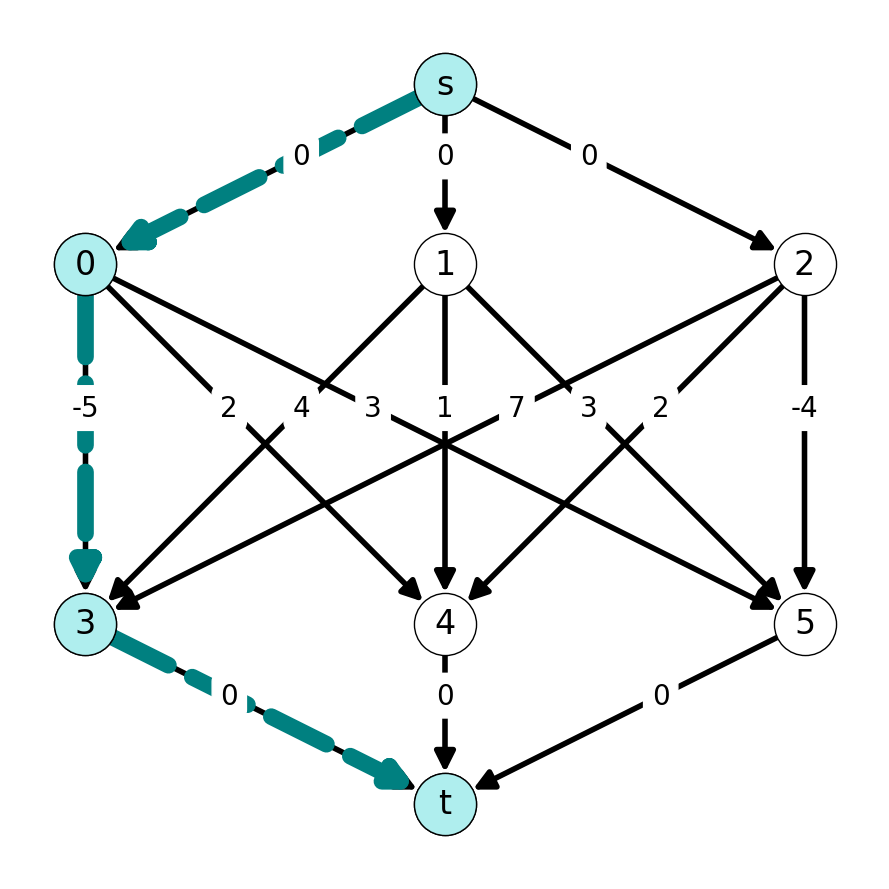
Figure 8.19: Graph $G$ corresponding to the assignment problem with costs $A$.

Step 1

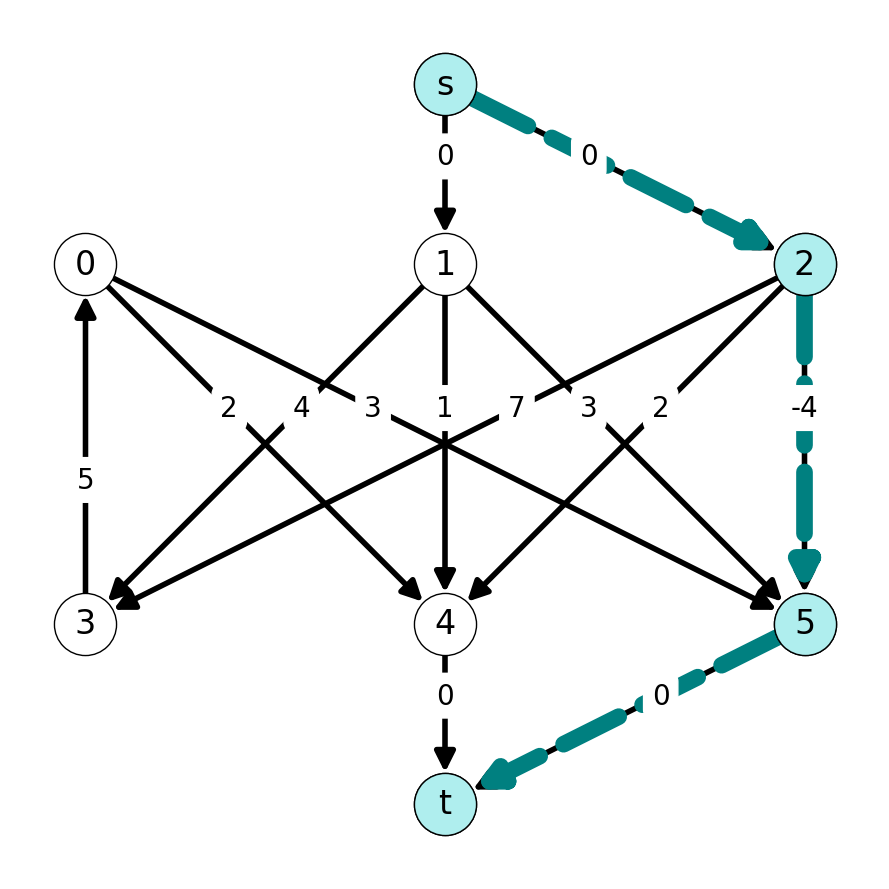
We construct the auxiliary graph $G'$ corresponding to the initial matching $M_0$ with $0$ edges. The shortest $st$-path in $G'$ is $(s,0,3,t)$. We use the subpath $P_0 = (0,3)$ to compute $M_1$: \[ M_1 = M_0 \Delta P_0 = \{03\}; \;\;\; w(M_1) = 5. \]

Step 2

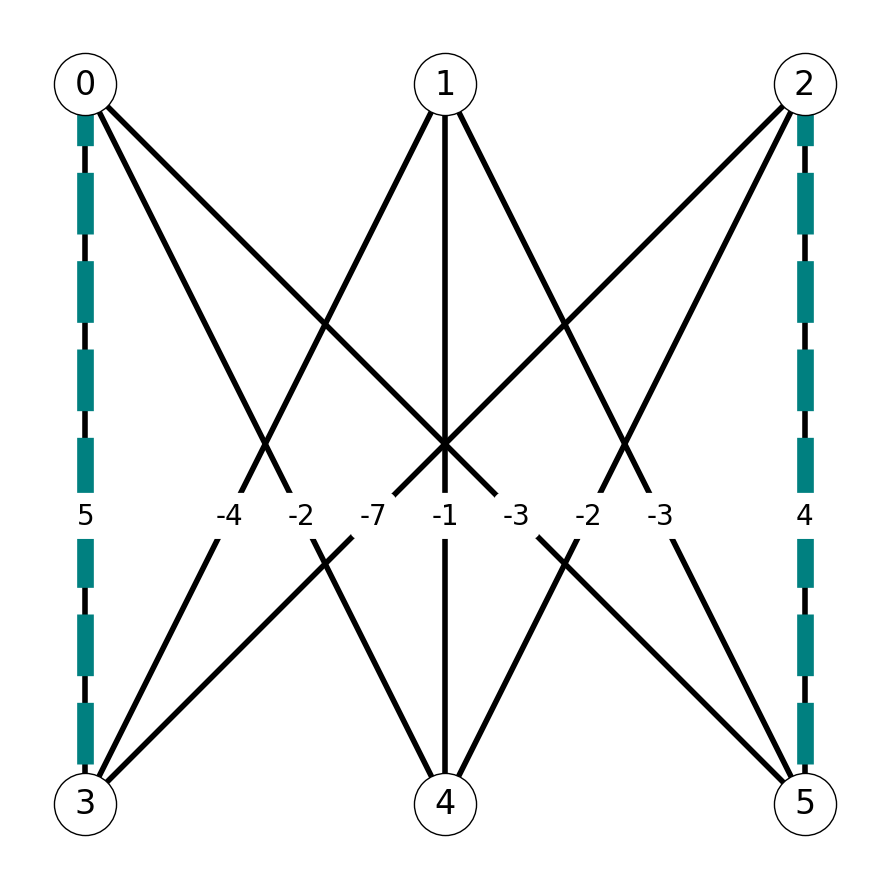
After updating the auxiliary graph, we see that shortest $st$-path in $G'$ is $(s,2,5,t)$. We let $P_1 = (2,5)$ and set \[ M_2 = M_1 \Delta P_1 = \{03, 25\}; \;\;\ w(M_2) = 9. \]

Step 3

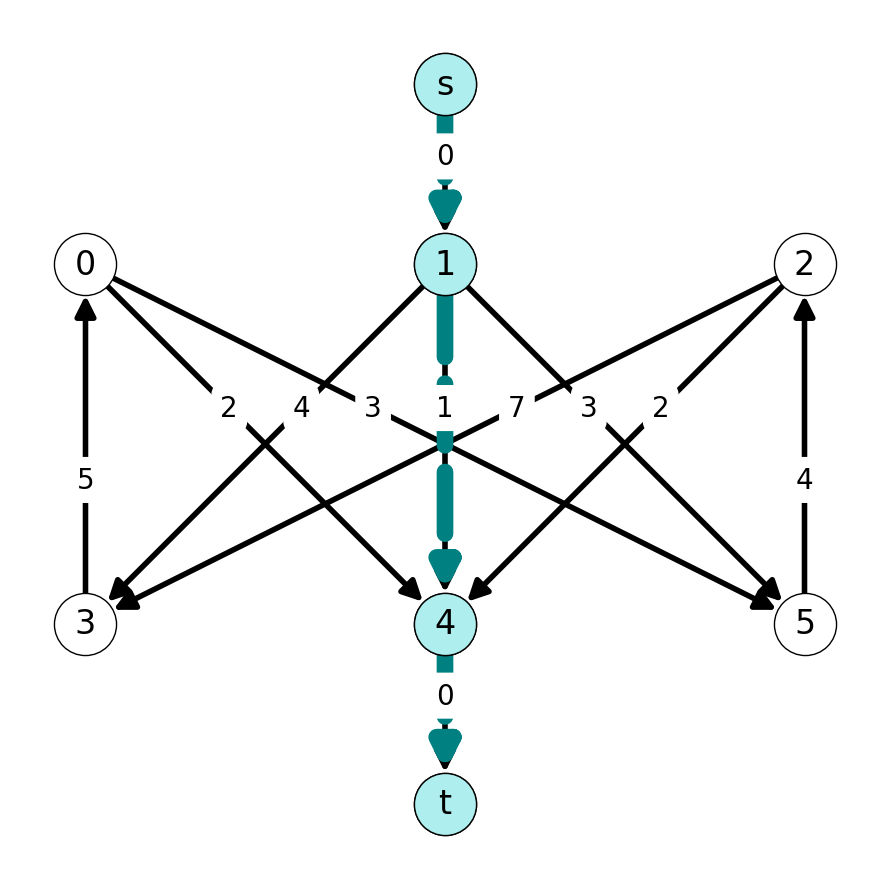
The shortest $st$-path in the auxiliary graph $G'$ with respect to $M_2$ is $(s, 1, 4, t)$. We let $P_2 = (1,4)$ and obtain the matching \[ M_3 = M_2 \Delta P_2 = \{03, 25, 14\} \] with $w(M_3) = 9 - 1 = 8$.

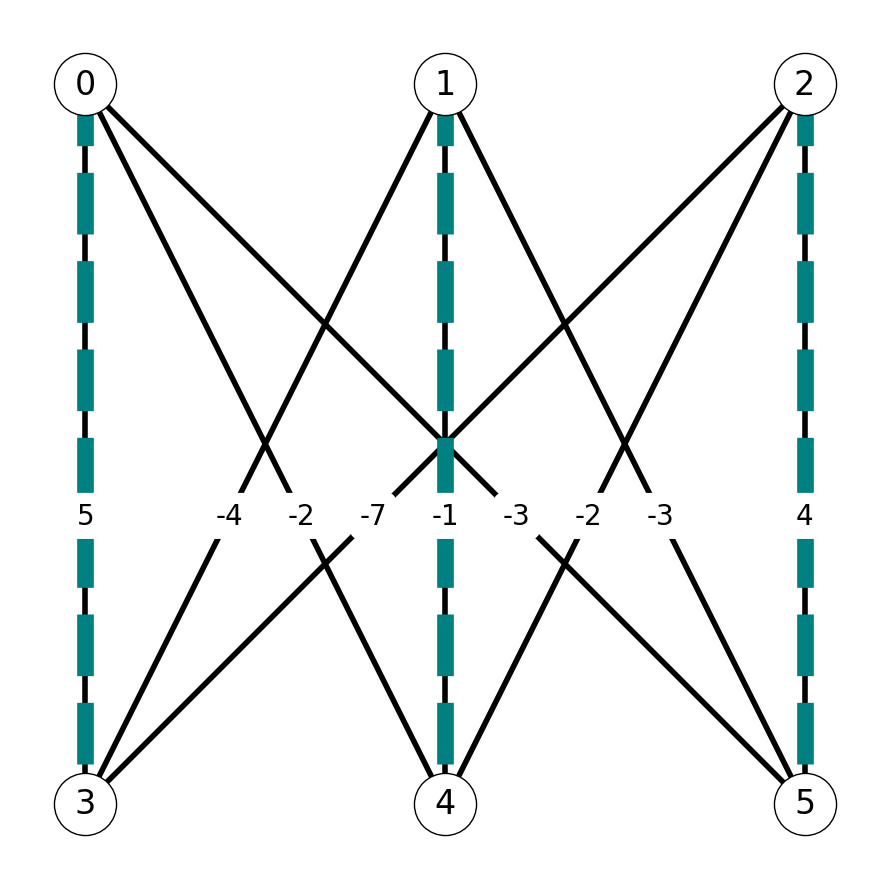
Termination

Since $\nu(G) = 3$, we stop the algorithm.

The maximum weight matching is $M_2$ with $w(M_2) = 9$.
The minimum cost assignment is given by $M_3$: \[ \pi(0) = 0,\;\;\; \pi(1) = 1, \;\;\; \pi(2) = 2 \] with minimum cost \[ \sum_{i=0}^2 a_{i, \pi(i)} = a_{11} + a_{22} + a_{33} = - w(M_3) = -8. \]